

Phyllotaxis is the study of plant patterns. Despite their diversity similar patterns are found in many different types of plants. Naturally this is due to the fact that many plants follow the same pathways during their early stages of development. A common eye catching pattern consists of two sets of spirals forming a lattice. This can be seen in the stamens of flowers (e.g. the male Leucadendron Discolor shown at the right), the florets of compound flowers (e.g. the Calendula shown below), the scales of pine cones, cycads, and seed ferns. This pattern is known as Spiral Phyllotaxis
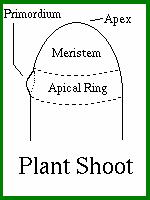
At the tip of a plant shoot are meristematic tissues, i.e. regions containing undifferentiated cells. These meristems are responsible for the production of the plant's organs such as leaves, thorns, tendrils, sepals, petals, etc. Near the boundary of the meristem is a region called the apical ring. Its in this region that new plant organs are formed. It usually takes a microscope to observe the process. Plant organs begin when cells in a spot along the apical ring undergo extensive cell divisions resulting in a bump, called a primordium, on the side of the apical ring. The phyllotactic pattern exhibited by the primordia is preserved as they develop into the various plant organs. Therefore with a good model of meristematic development we can account for the phyllotactic patterns found in nature.
Around the turn of the 18th century the well known Astronomer Johannes Kepler observed that the Fibonacci numbers are common in plants. And around 1790 Bonnet pointed out that in spiral phyllotaxis the number of spirals going clockwise and counter-clockwise were frequently two successive Fibonacci numbers. For example the orange Calendula shown below has 13 spirals going in one direction and 21 spirals going in the other direction.

Here is a Calendula officinalis from my garden. The capitulum is about 1cm in diameter. The florets along the margin of the capitulum have just recently opened while those in the center still have a touch of green. The capitulums of compound flowers such as Calendula, Asters, Mums, Daisies, and Sunflowers are well known to produce nice examples of spiral phyllotaxis. The number of spirals observed in a plant organ like a flower is known as the "parastichy numbers". In this case the parastichy numbers are (13,21).

|
On the left we see 21 blue spirals moving inward in a clockwise fashion and on the right we see 13 white spirals moving inward in a counter-clockwise fashion.

|

|
The Fibonacci numbers are prevalent throughout much of the plant kingdom and understanding why has become a interdisciplinary effort. Several ideas have been proposed over the years. Many of them have been based on the notion that the Fibonacci numbers somehow promote the survival of mature plants. Among the suggestions on how Fibonacci numbers could promote survival are: by providing dense packings of seeds, by allowing circulation of air through leaves, and by allowing light to fall on as many leaves as possible.

|

|
A more modern view is that a common physical condition occurs in the early stages of development that constrains the structure of the flower to follow the Fibonacci pattern. The point of the Fibonacci numbers does not lie in some activity performed by a mature plant but in the activity which occurs during development. The Fibonacci numbers are not seen as doing very much to promote or hinder survival in mature plants. A Calendula whose flowers have 12 spirals going in one direction and 22 going in the other direction should have about the same chance of producing viable seeds for the next generation as one whose flowers have 13 spirals going in one direction and 21 in the other direction. Yet the first case is virtually unheard of while the second case is very common.
But what is the nature of this constraint? An important result occurred in
1992 when two French Physicists, Douady and Couder, developed a laboratory
model of plant development. To learn more see the website I helped build:
Phyllotaxis: An Interactive Site
for the Mathematical Study of Plant Pattern Formation.
Send comments or suggestions to
scotton
at
sdf
dot
lonestar
dot
org
